Find the Volume of the Ellipsoid by Relating It to a Volume You Know

Mensuration is a sub-branch of mathematics that is used to talk over different types of geometrical shapes like cube, cylinder, ellipsoid, their areas, and volume. Information technology is used to find the geometric and algebraic equations that are used to measure various aspects of objects or shapes like Expanse, Volume, Curve Surface expanse, etc. In mensuration, volume is used to calculate the amount of space inside a 3D object that tin can be filled. We tin can find the volume of any solid object like foursquare, cylinder, ellipsoid, etc. In this article, we will learn how to calculate the book of the Ellipsoid.

Ellipsoid

Ellipsoid is a three-dimensional geometric figure. It is a closed surface in an elliptical shape and is seen as a structured ellipse. It gets its name from the ellipse considering any airplane that cuts through the ellipsoid will form an ellipse. Information technology has three axes of rotational symmetry and these three axes are perpendicular to each other and run across at 1 bespeak which is known as the center of the ellipsoid.  Ellipsoid are of two types:

• Oblate Ellipsoid: If a = b and a > c, and then such type of ellipsoid is known every bit Oblate ellipsoid.
• Prolate Ellipsoid: If a = b and c > a, then such type of ellipsoid is known as a prolate ellipsoid.

The standard equation of ellipsoid is

10²/a² + yⁱⁱ/b² + z²/c^two = one

Here a ≠ b ≠ c. If a = b = c and so that ellipsoid is known equally a sphere.

Volume of the Ellipsoid

The book of the ellipsoid is the measurement of the ellipsoid that expresses the corporeality of three-dimensional space enclosed by a airtight surface.

Equally we know that the equation of ellipsoid be (x²/a^two) + (y²/b²) + (z²/cⁱⁱ) = one where a, b, c are the lengths of semi-axes of ellipsoid then volume tin can be calculated by the below formula-

Volume of Ellipsoid = (4/3) × π × a × b × c

The volume of Oblate Ellipsoid is

Volume of Oblate Ellipsoid = (four/3) × π × a × a × b

The book of Prolate Ellipsoid is

Volume of Prolate Ellipsoid = (4/3) × π × a × b × b

Case:

Given the length of semi-axes are 5cm, 6cm, 4cm

And then the volume of the ellipsoid is

V = (iv/three) × π × a × b × c

= (4/3) × π × five × half dozen × four

= 430/3

= 160

Hence the volume of the ellipsoid is 160

Determining the book of the ellipsoid

As we know that the equation of ellipsoid is

(ten²/a²) + (y²/bⁱⁱ) + (z²/c^two) = 1

Allow united states assume that -a ≤ x ≤ a

Now, we cut the ellipsoid with a plane parallel to the yz-plane

So, we get an ellipse

(y^two/b²) + (z²/cⁱⁱ) = i – (ten^two/a²)

(y²/b²(1 – (ten²/aⁱⁱ))) + (zⁱⁱ/c²(one – (x²/aⁱⁱ) )) = i

So the semiaxes are

p = b√(one – (x²/a²)) and q = c√(1 – (10²/a²))

As we know that the area of ellipse is

A(x) =  πbc(1 – (xⁱⁱ/a²)) …..(ane)

Now past using the formula of parent entry nosotros summate the volume of the ellipsoid

V = \limi

Now put the value of A(ten) fro equation (one), we get

V = πbc \limi

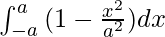
V = 4/3πbc

Sample Questions

Question ane: Find the book of the ellipsoid if the lengths of semi-axes are 3cm, 4cm, 2cm.

Solution:

Given,

Lengths of semi axes of an ellipsoid a=3cm, b=4cm, c=2cm

Volume = (iv/3) × π × a × b × c

= (4/three) × π × three × 4 × 2

= 32 × π

= 100.53 cmⁱⁱⁱ

And so, volume of ellipsoid with given measurements is 100.53cm^three.

Question 2: Find the volume of the ellipsoid if the lengths of semi-axes are 5cm, 3cm, 2cm.

Solution:

Given,

Lengths of semi axes of an ellipsoid a = 5cm, b = 3cm, c = 2cm

Volume = (4/three) × π × a × b × c

= (iv/3) × π × 5 × three × 2

= forty × π

= 125.66 cmⁱⁱⁱ

Then, volume of ellipsoid with given measurements is 125.66cm³.

Question 3: Find the book of the ellipsoid if the lengths of axes are 6cm, 4cm, 2cm.

Solution:

Given,

Lengths of axes of an ellipsoid are 6cm, 4cm and 2cm.

Length of semi axes = Length of axes/2

a = (6/two) = 3cm

b = (4/ii) = 2cm

c = (2/two) = 1cm

Volume = (four/3) × π × a × b × c

= (4/3) × π × 3 × 2 × 1

= 8× π

= 25.xiii cm³

And then, book of ellipsoid with given measurements is 25.13cm^three.

Question 4: Discover the volume of the ellipsoid if the lengths of axes are 12cm, 6cm, and 2cm.

Solution:

Given,

Lengths of axes of an ellipsoid are 12cm, 6cm and 2cm.

Length of semi axes = Length of axes/ii

a = (12/2) = 6cm

b = (vi/2) = 3cm

c = (ii/ii) = 1cm

Volume = (4/3) × π × a × b × c

= (4/3) × π × vi × 3 × 1

= 24× π

= 75.iv cm³

So, the book of ellipsoid with given measurements is 75.4cm³.

Question five: Observe the volume of ellipsoid if the equation is given every bit (10²/vii^two) + (y^two/iv²) + (z²/2²) = ane

Solution:

Given,

Equation of ellipsoid, (x²/vii²) + (yⁱⁱ/4²) + (z²/2ⁱⁱ) = 1

Information technology is of course (x^two/a²) + (y²/bⁱⁱ) + (z²/c²) = one

From this we tin can derive lengths of semi axes.

a = 7

b = 4

c = two

Volume = (four/3) × π × a × b × c

= (4/three) × π × seven × 4 × ii

= (224/3) × π

= 234.57 cm³

Then, the book of ellipsoid with given measurements is 234.57cm^three.

linniumber55.blogspot.com

Source: https://www.geeksforgeeks.org/how-to-calculate-the-volume-of-an-ellipsoid/

Share this post